Gear Parameter

• Print
• Email

Module

The division of the tooth pitch divided by Pi is called module (in mm). The commonly used modules are transverse module, normal module and axial module. They are artificial given geometries set to provide convenience for gear design, calculation, manufacturing and inspection and make the gear system more systematized, standardized and generalized. At present, different countries or different gear types have their own standard module value. Most of their sizes are indicated by the series of preferred numbers--R10, R20.

Gear taking module as its length measurement unit is called “module system gear”. What china uses is modulus system gear.

Transverse Module

The division of transverse circular pitch divided by Pi is called transverse module. The relation between transverse module and normal module is: m_t=m_n/cosß; the relation between transverse module and axial module is:m_t=m_xtgß.

Axial Module

The division of axial pitch divided by Pi is called axial module (in mm). The relation between axial module and normal module is:m_x=m_n/sinß; the relation between axial module and transverse module is:m_x=m_t/tgß.

Normal Module

The division of normal pitch divided by Pi is called normal module (in mm). The relation between normal module and transverse module is:m_n=m_tcosß; the relation between normal module and axial module is:m_n=m_xsinß.

Diametral Pitch

The standard definition of diametral pitch in GB3374—82 is: The quotient calculated in the division that Pi is divided by pitch (in mm) is called diametrical pitch. This value is equal to the inverse of module.

Gear taking diametral pitch P as geometric measurement unit is called “gears measured by diametral pitch”. Gears measured by diametral pitch are mostly used in countries where imperial units are used. In these countries, diametral pitch is defined as the quotient calculated through the gear teeth dividing by the diameter (in in).  At this time, the relation between the module and diametral pitch is P=25.4／m.

Transverse Diametral Pitch

The transverse diametral pitch means the quotient calculated through which Pi is divided by the transverse circular pitch. This value is equal to the inverse of transverse module. The relation between transverse diametral pitch and normal diametral pitch is:P_t=P_n/cosβ. The relation between the transverse diametral pitch and axial diametral pitch is: Pt=Pxtgβ.

Axial Diametral Pitch

The axial diametral pitch means the quotient calculated through which Pi is divided by the axial pitch (in mm). This value is equal to the inverse of the axial module. The relation between the axial diametral pitch and the transverse diametral pitch is: Px=Pt/tgβ; the relation between the axial diametral pitch and normal diametral pitch is: Px=Pn/sinβ.

Normal Diametral Pitch

The normal diametral pitch means the quotient calculated through which Pi is divided by normal pitch (in mm). This value is equal to the inverse of normal module. The relation between normal diametral pitch and transverse diametral pitch is: P_n=P_tcosβ. The relation between normal diametral pitch and axial diametral pitch is: P_n=P_xsinβ.

Metric Gear

Metric gear takes module as its length measurement unit. What China uses is metric gear.

Double Modulus Gear

Double modulus gear takes two kinds of module as its unit for geometric measurement.

DP gear

Gear taking pitch as its unit for geometric measurement is called pitch gear, also known as diametral pitch gear (DP gear).

Double Diameter Pitch Gear

The definition of double diametral pitch gear and the method of its calculation is the same as double module gear. See “double module gear”.

Addendum Coefficient

The addendum coefficient means the quotient calculated through which the addendum of standard gear is divided by modulus, namely h*_a=h_a/m. According to GB1356-87, the normal tooth is h^*_a=1.

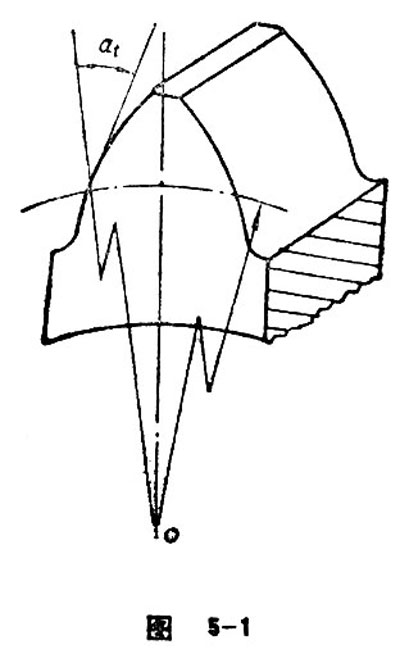
Transverse Pressure Angle

In the gear end plane and the intersection point of the transverse tooth profile and the reference circle, there is an acute angle formed between the radial diameter and the tangent existing at the point of the intersection. This acute angle is called transverse pressure angle (see figure 5-1). The relation between the transverse pressure angle and normal pressure angle is: tga_t=tga_ncosß.

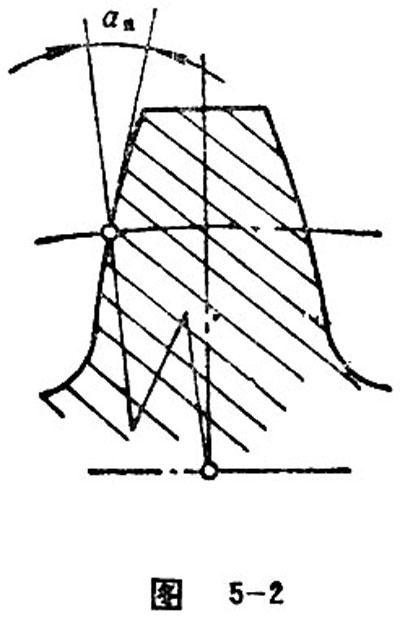
Normal Pressure Angle

On the tooth of a gear, the acute angle formed by the intersection of an radial line found at a point of tooth trace and the tangent plane at the same point of this tooth flank is called normal pressure angle (see figure 5-2). The relation between normal pressure angle and transverse pressure angle is: tga_n=tga_tcosß

Transverse Pressure Angle at a Point

In gear end plane, the acute angle formed by the intersection of a radial line at any point M on the transverse tooth profile and the tangent at the same point is called transverse pressure angle at a point.

Normal Pressure Angle at a Point

The acute angle formed by the intersection of a radial line at a point of the tooth surface and the tangent at the same point is called normal pressure angle at a point.

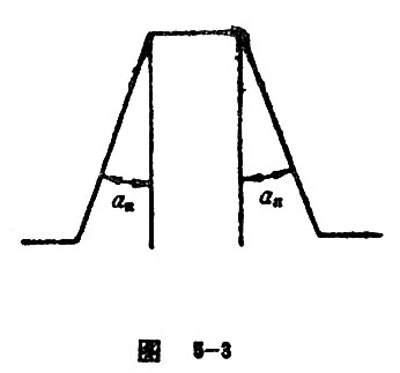
Nominal Pressure Angle

The normal pressure angle of basic rack is called normal pressure angle (see Figure 5-3). According to GB1356-88, the normal pressure angle is a_n=20^。. Some countries adopt the angle 14.5^。and 15^。. Currently, extensive research has been carried out on gear with large nominal pressure angle, such as a_n=25^。、28^。、30^。.

Researches show that this kind of gear has great advantage in loading capacity.

Big Pressure Angle

Big pressure angle refers to those normal (end surface or axial) pressure angle whose pressure angle is greater than 20^。. Big pressure angle can do benefits to gear’s bending strength and contact strength but not to the bearing. The adopted big pressure angles nowadays are 25^。、27^。、28^。、30^。  etc.

Small Pressure Angle

Small pressure angle refers to normal pressure angle whose pressure angle is less than 20^。.